A weighted average is most often computed to equalize the frequency of the values in a data set. The survey team could weight the results of the 18-to-34 age group so that their views are represented proportionately. Then, consider this as the term and multiply that by $0.4$ when calculating the weighted average of the grade. A weighted average, on the other hand, is better when values have different amounts of worth or weight.

Example 2

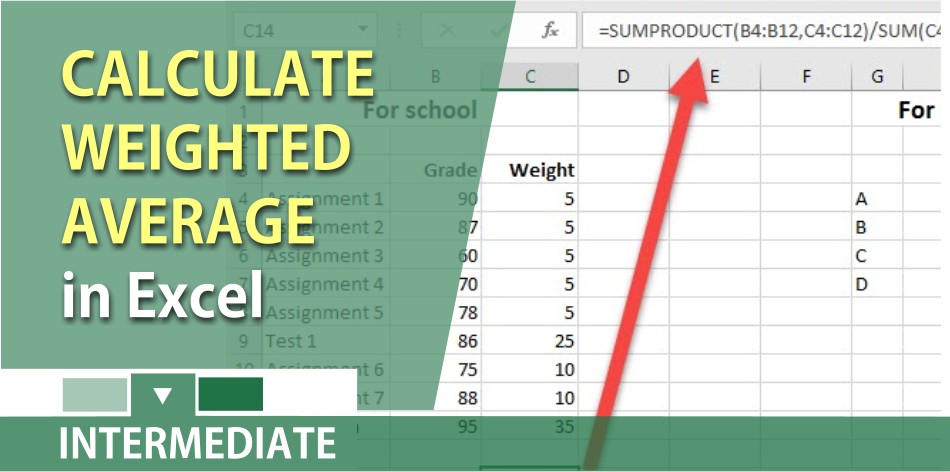
As the name suggests, a weighted average is one where the different numbers you’re working with have different values, or weights, relative to each other. For example, you may need to find a weighted average if you’re trying to calculate your grade in a class where different assignments are worth different percentages of your total grade. The procedure you use will be a little different depending on whether or not your total weights add up to 1 (or 100%). The weighted average of the written test will be 0.5, the practical test will be 0.3, and sports will be 0.2. Also, if a value has the highest weight, then it will have more effect on the weighted average and vice-versa.

Frequently Asked Questions on Weighted Average (FAQs)

In this example, the quizzes are for 25%, the performance assignments are worth 45%, and the final exam is worth 30%. Convert the percentages to decimal form to identify the weighting factors. The term “weighted average” refers to an average in which each quantity is to be averaged given a weight. The step after numbers are multiplied by weights is the same for both unweighted and weighted averages.

Real-Life Examples on Weighted Average

The weighted average formula is used to calculate the mean weighted value of the data with n terms. In the case of stock market accounting, this method helps a lot as it smoothes all kinds of fluctuations in the market. In normal methods, often, some sections are either over-represented or under-represented.

The weighted average method ensures that more significant numbers have a greater impact on the final average, making the weighted average a more accurate reflection of the data set. When some quantities are more important than the others and do not contribute equally to the final result thus multiplying them to a coefficient is called weighted average. It is a simple process of deriving at an average value between two or quantities when weight is added to it. For example, a student realizes that the scores after an exam is two times more important than the scores acquired during the quiz.

Related AccountingTools Courses

Weighted Average is a method of finding the average of a set of numbers where each number (or data point) is given a weight based on its importance or relevance. Weighted averages are commonly used in various fields such as finance, economics, education, and statistics, where different data points may have different levels of importance. This is the sum of the products of terms and their corresponding weights divided by the sum of the weights.

If rounding in the middle is needed, keep the number of decimal places the same to cut down on rounding errors over time. When making key decisions, it’s best to double-check your calculations and keep a record of the original, unrounded numbers for future use. The student’s final grade averaged 89.5, reflecting the different weights of each educational component in the formula. Normally, when computing an average, each data point carries the same weight.

• Weighted average is one of the most commonly employed measures in statistical data to find the average of quantities when each quantity has a certain weight.
• This makes them particularly useful in finance for calculating compound interest rates or in epidemiology for analyzing disease spread rates.
• The weighted average formula is the summation of the product of weights and quantities, divided by the summation of weights.
• We can compute this using our average calculator, by hand, or by using a hand-held calculator since all the values have equal weights.
• To calculate the weighted average, multiply each term by its weight, then divide by the sum of the weights.

( b ) 10 weighted 25, 12 weighted 30, 16 weighted 20, and 15 weighted at 5. ( a ) 5 weighted at 20%, 7 weighted at 65%, and 8 weighted at 15%. ( a ) 5 weighted at 20%, 7 weighted at 65%, and 8 weighted at 15%.( b ) 10 weighted 25, 12 weighted 30, strong letter for outstanding payment templates 16 weighted 20, and 15 weighted at 5. Weighted average calculations are used in many other jobs, such as by funding specialists and actuaries. This is true in situations such as calculating the benefits the average unemployed person receives.

Often in survey works such as census data, a segment of a population is either over-represented or under-represented. In such a situation, the weighted average takes the uneven population into consideration and turns them into a more balanced and equal representation of the data. This is basically done when the data deals with demographics and population size.

This formula represents the ratio of the sum of the products of each value (x) and its equal weight (w) to the sum of the weights. It’s just summing all scores and dividing the result by the total number of observations (4 courses). To figure out how to calculate a weighted average, we need to know the weight of each value. Typically, we present the weights in the form of a percentage or (in statistics) a probability of occurrence. Sometimes it may be a really significant difference – like a grade difference or even whether you pass or fail your course. For example, a teacher evaluates a student based on exam results, project work, attendance, and classroom behavior.

The numbers that must be arranged refer to the grades you obtained in your quizzes, performance tasks, and final exam. A normal average calculation would completely miss this detail or require more data to provide the same accurate look. A normal average calculation would not be useful, as it would not account for these different volumes. Listed below are a few topics that are related to a weighted average. Weighted average are usually used for quantitative data, but can indeed lean over to the qualitative side or talk along it by taking numerical scores of qualitative categories.